7.Logica

Proposiciones

Una proposición matemática es una expresión algebraica que puede tener dos valores: ser verdadera o ser falsa, aunque nunca ambas a la vez. Denominadas a través de letras minúsculas, tienen un valor de verdad (que sera la veracidad o la falsedad de su enunciado).

De acuerdo a sus características, es posible distinguir entre proposiciones simples (que carecen de conectores lógicos) y proposiciones compuestas (cuentan con mas de un conector lógico).

Las proposiciones matemáticas pueden ser vistas como expresiones de juicio que no pueden resultar verdaderas y falsas de manera simultanea. Por ejemplo:

a: 9 es múltiplo de 3

Dicha expresión es una proposición matemática resulta verdadera, ya que 3x3 es igual a 9 y por lo tanto, 9 es uno de los infinitos múltiplos de 3. Como decíamos, la proposición matemática puede ser falsa:

b: 7 es múltiplo de 3

En este caso la proposición falsa por que 7 no es múltiplo de 3.

   Proposicion matematica abierta: Es aquella que su valor de verdad no cambia. Por ejemplo:

a: Quito es la capital de Ecuador   (V)

b: La luna es un planeta                 (F)
c: 2+5=9                                         (F)

   Proposicion matematica cerrada: Es aquella que su valor de verdad no esta definido y depende de un conjunto referencial. Por ejemplo:

a: Hoy va a llover; puede ser verdadera o falsa, no tiene conjunto referencial que la defina.

   Proposicion matematica simple o atomica: Es aquella que no esta unida con otra preposicion. Por ejemplo: 

a: Quito es la capital de Ecuador

b: La luna es un planeta

c: 2+5=9

   Proposicion matematica compuesta o molecular: Son proposiciones que se obtienen de la combinacion de dos o mas proposiciones simples mediante los colectivos u operadores logicos. Por ejemplo:

*9 es multiplo de 3 y 10 es multiplo de 2

*El gusano es invertebrado o vertebrado

*16 es multiplo de 4 entonces 4 es multiplo de 2

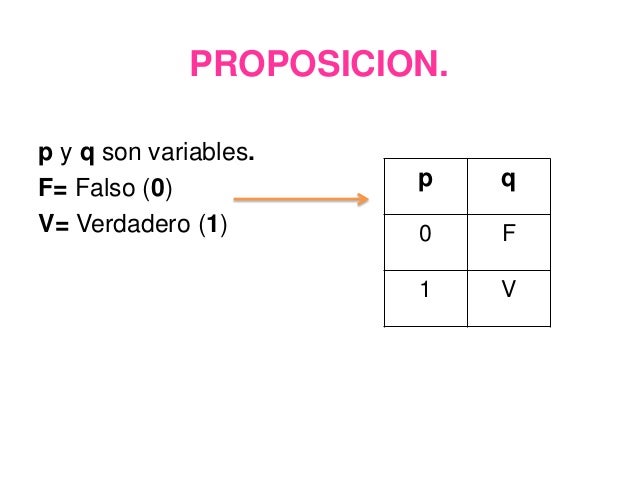
    Valores de verdad: Se llama valor de verdad de una proposicion a la verdad o a la falsedad de su contenido.

Cuantificadores

Un cuantificador es una expresion que indica la cantidad de veces que un predicado o propiedad P se satisface dentro de una determinada clase, se usa el simbolo ∃ llamado cuantificador existencial, antepuesto a una variable para decir "existe". Existen muchos tipos de cuantificadores, entre los mas utilizados estan:

   Cuantificador universal: Se utiliza para afirmar que todos los elementos de un conjunto cumplen con una determinada propiedad. Por ejemplo:

Para todo (x) perteneciente a A, se cumple P (x)

Esta afirmacion suele usarse como la equivalente de la proposicion siguiente:

Se define el conjunto A, como el de los elementos x de U que cumplen P (x)

   Cuantificador existencial: Se usa para indicar que hay uno o mas elementos en el conjunto A que cumplen una determinada propiedad. Se escribe:

∃x∈A:P(x)

Existe x en A que cumple P (x)

Esta proposicion suele interpretarse como la equivalente de la proposicion siguiente:

{x∈A:P(x)}≠∅

El conjunto de los elementos x de A, que cumplen P (x) es distinto del conjunto vacio.

   Cuantificador existencial unico: Se usa para indicar que hay un unico elemento de un conjunto A que cumple una determinada propiedad. Se escribe:

∃!x∈A:P(x)

 Existe una unica x elementos de A 

Tablas de la verdad

Una tabla de la verdad es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar. Sus tipos son:

   Verdad indeterminada o contingencia

Se entiende por verdad contingente, o verdad de hecho, aquella proposición que puede ser verdadera o falsa, según los valores de las proposiciones que la integran. Sea el caso: ${\displaystyle A\land (B\lor C)}$.

Su tabla de verdad se construye de la siguiente manera:

Ocho filas que responden a los casos posibles que pueden darse según el valor V o F de cada una de las proposiciones A, B, C.



   Contradicción

Se entiende por contradicción aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es F.

   Tautologías

Se entiende por tautología aquella proposición que en todos los casos posibles de su tabla de verdad su valor siempre es V.

   Proposición condicional





Si se conectan dos enunciados colocando la palabra "si" antes de la condición y después de la palabra "entonces", la proposición resultante se llama un condicional. Por ejemplo:

 1) p(x): x es un número entero, y
2) q(x): x es un número racional.