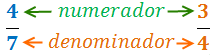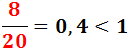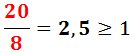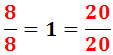Potenciacion
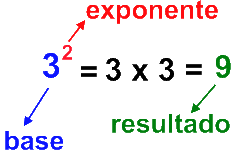
La potenciacion es una forma abreviada de escribir un producto formado por varios factores iguales. La base de una potencia es el numero que multiplicamos por si mismo.
Sus propiedades
1. Un numero elevado a 0 es igual a 1.
a0 = 1
2. Un numero elevado a 1 es igual a si mismo.
a1 = a
3. Producto de potencias con la misma base.
Es otra potencia con la misma base y cuyo exponente es la suma de los exponentes.
am · a n = am+n
4. División de potencias con la misma base
Es otra potencia con la misma base y cuyo exponente es la diferencia de los exponentes.
am : a n = am - n
5. Potencia de una potencia
Es otra potencia con la misma base y cuyo exponente es el producto de los exponentes.
(am)n = am · n
6. Producto de potencias con el mismo exponente
Es otra potencia con la misma base y cuya base es el producto de las bases.
an · b n = (a · b) n
7. Cociente de potencias con el mismo exponente
Es otra potencia con el mismo exponente y cuya base es el cociente de las bases.
an : bn = (a : b)n
Radicacion
La radicacion es el proceso de hallar raíces de orden
n de un numero
a, de modo que se verifica que

donde
n es llamado indice u orden, a es llamado radicando y
x es una raíz enésima.
Sus propiedades
1. Raíz de un producto
La raíz de un producto es igual al producto de las raíces de los factores.
2. Raíz de un cociente
La raíz de una fracción es igual al cociente de la raíz del numerador entre la raíz del denominador.
3. Raíz de una raíz
Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva el radicando.
Logaritmacion
El logaritmo de un numero real positivo es el exponente al cual hay que elevar la base para obtener dicho numero.
Sus propiedades
1. El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
2. El logaritmo de un cociente es igual al logaritmo del numerador menos el logaritmo del denominador.
3. El logaritmo de una potencia es igual al producto entre el exponente y el logaritmo de la base de la potencia.
4. El logaritmo de una raíz es igual al producto entre la inversa del índice y el logaritmo del radicando.
-






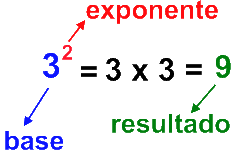
 donde n es llamado indice u orden, a es llamado radicando y x es una raíz enésima.
donde n es llamado indice u orden, a es llamado radicando y x es una raíz enésima.![\sqrt[n]{{a} \cdot {b}} = \sqrt[n]{a} \cdot \sqrt[n]{b}](https://upload.wikimedia.org/math/6/2/f/62ff232d8ae597f13efb5db26edc04cb.png)




![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/903e79991b966e9c9825f9cf3aaa87748810e236)